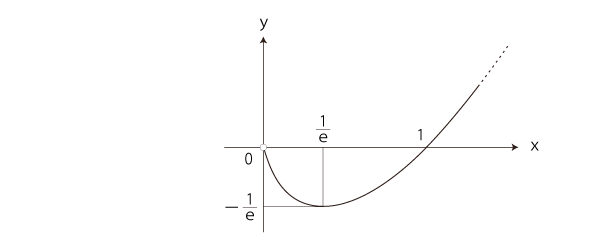
y= (1ーx) log (1ーx) は,つぎの3つの関数を順に合成したもの:
x├─→ xー1
x├─→ ーx
x├─→ x log x
よって,y= (1ーx) log (1ーx) のグラフは,y=x log x のグラフを y軸で折返し,そしてx軸の正方向に1ずらしたもの:
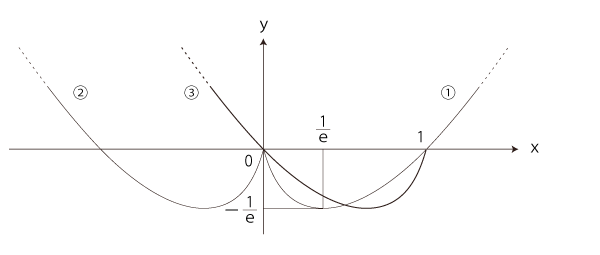
こうして,つぎが y=x log x + (1ーx) log (1ーx) のグラフになる:
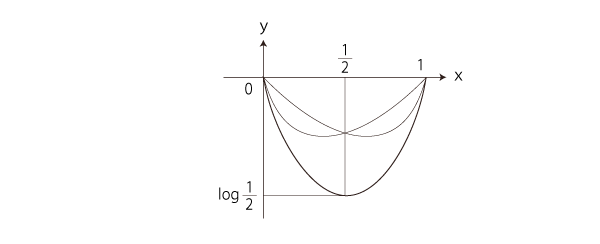
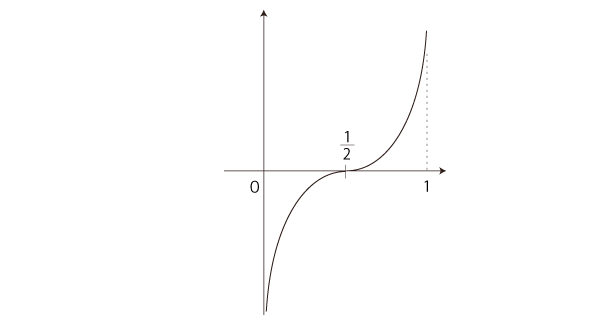
グラフの傾きの変化も,押さえておくとしよう。
\[
\begin{align}
\frac{ dy }{ dx }
&= \frac{ d }{ dx }\ ( x\ log\ x + ( 1 - x )\ log\ ( 1 - x ) ) \\
&= log\ x + x \frac{ 1 }{ x } + (-1)\ log\ ( 1 - x ) ) + ( 1 - x ) \frac{ - 1 }{ 1 - x } \\
&= log\ x +1 - log\ ( 1 - x ) - 1 \\
&= \ log\ x - log\ ( 1 - x ) \\ \\
&=
\begin{cases}
log\ \frac{ x }{ 1 - x } \ \ \rightarrow + \infty \ \ ( x \rightarrow 1 ) \\
- log\ \frac{ 1 - x }{ x } \ \ \rightarrow - \infty \ \ ( x \rightarrow 0 )
\end{cases}
\end{align}
\]
|







